Graf funkce gama pro reálná čísla. Gama funkce (někdy také označovaná jako Eulerův integrál druhého druhu ) je zobecněním faktoriálu pro obor komplexních čísel . Používá se v mnoha oblastech matematiky , např. pro popis některých rozdělení pravděpodobnosti .
Funkce je značena pomocí řeckého písmene gama a je definována jako holomorfní rozšíření integrálu:
Γ ( z ) = ∫ 0 ∞ t z − 1 e − t d t {\displaystyle \Gamma (z)=\int _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\,\mathrm {d} t} Ačkoliv integrál samotný konverguje jen, je-li reálná část z kladná, gama funkce je definována pro libovolné komplexní číslo, kromě nekladných celých čísel .
Vlastnosti
Funkce Γ {\displaystyle \Gamma } spojitá pro z > 0 {\displaystyle z>0} Γ {\displaystyle \Gamma } z ≤ 0 {\displaystyle z\leq 0} póly prvního řádu a odpovídající rezidua jsou Res z = k , k ∈ Z , k ≤ 0 Γ ( z ) = ( − 1 ) − k Γ ( − k ) {\displaystyle \operatorname {Res} _{z=k,k\in \mathbb {Z} ,k\leq 0}\Gamma (z)={\frac {(-1)^{-k}}{\Gamma (-k)}}} meromorfní v celém oboru C {\displaystyle \mathbb {C} }
Pro n -tou derivaci platí vztah
Γ ( n ) ( z ) = ∫ 0 ∞ t z − 1 e − t ln n t d t {\displaystyle \Gamma ^{(n)}(z)=\int \limits _{0}^{\infty }t^{z-1}\mathrm {e} ^{-t}\ln ^{n}t\,\mathrm {d} t} V oblasti kladných reálných čísel má gama funkce minimum v bodě x ≈ 1,461 6 {\displaystyle x\approx 1{,}461\,6}
Pro přirozená čísla n {\displaystyle n} Γ ( n ) = ( n − 1 ) ! {\displaystyle \Gamma (n)=(n-1)!\,}
Γ ( z + 1 ) = z Γ ( z ) {\displaystyle \Gamma (z+1)=z\Gamma (z)\,} Γ ( z ) Γ ( 1 − z ) = π sin π z pro 0 < z < 1 {\displaystyle \Gamma (z)\Gamma (1-z)={\frac {\pi }{\sin {\pi z}}}\;{\mbox{ pro }}0<z<1} Γ ( z ) Γ ( z + 1 2 ) = π 2 2 z − 1 Γ ( 2 z ) {\displaystyle \Gamma (z)\Gamma (z+{\frac {1}{2}})={\frac {\sqrt {\pi }}{2^{2z-1}}}\Gamma (2z)}
Γ ( − 2 ) {\displaystyle \Gamma (-2)\,}
(nedefinováno)
Γ ( − 3 / 2 ) {\displaystyle \Gamma (-3/2)\,}
= 4 π 3 {\displaystyle ={\frac {4{\sqrt {\pi }}}{3}}\,}
Γ ( − 1 ) {\displaystyle \Gamma (-1)\,}
(nedefinováno)
Γ ( − 1 / 2 ) {\displaystyle \Gamma (-1/2)\,}
= − 2 π {\displaystyle =-2{\sqrt {\pi }}\,}
Γ ( 0 ) {\displaystyle \Gamma (0)\,}
(nedefinováno)
Γ ( 1 / 2 ) {\displaystyle \Gamma (1/2)\,}
= π {\displaystyle ={\sqrt {\pi }}\,}
Γ ( 1 ) {\displaystyle \Gamma (1)\,}
= 0 ! = 1 {\displaystyle =0!=1\,}
Γ ( 3 / 2 ) {\displaystyle \Gamma (3/2)\,}
= π 2 {\displaystyle ={\frac {\sqrt {\pi }}{2}}\,}
Γ ( 2 ) {\displaystyle \Gamma (2)\,}
= 1 ! = 1 {\displaystyle =1!=1\,}
Γ ( 5 / 2 ) {\displaystyle \Gamma (5/2)\,}
= 3 π 4 {\displaystyle ={\frac {3{\sqrt {\pi }}}{4}}\,}
Γ ( 3 ) {\displaystyle \Gamma (3)\,}
= 2 ! = 2 {\displaystyle =2!=2\,}
Γ ( 7 / 2 ) {\displaystyle \Gamma (7/2)\,}
= 15 π 8 {\displaystyle ={\frac {15{\sqrt {\pi }}}{8}}\,}
Γ ( 4 ) {\displaystyle \Gamma (4)\,}
= 3 ! = 6 {\displaystyle =3!=6\,}
lim z → 0 + Γ ( z ) {\displaystyle \lim _{z\to 0+}\Gamma (z)\,}
= + ∞ {\displaystyle =+\infty \,}
lim z → + ∞ Γ ( z ) {\displaystyle \lim _{z\to +\infty }\Gamma (z)\,}
= + ∞ {\displaystyle =+\infty \,}
Grafy
Zdroj
Poslední aktualizace obsahu: 2024-08-26 11:48:55
Zdroj: Wikipedia (autoři článku Funkce gama )
Licence textu: CC-BY-SA-3.0 Unported
Tento článek byl automaticky přejat z Wikipedie. Na obrázcích nebyly provedeny žádné změny. Obrázky se zobrazují ve zmenšené velikosti (jako miniatury). Kliknutím na obrázek získáte další informace o autorovi a licenci. Byly změněny prvky designu, odstraněny některé odkazy specifické pro Wikipedii (např. odkazy na Editaci a nebo na neexistující hesla) a provedena optimalizace pro rychlé načítání.
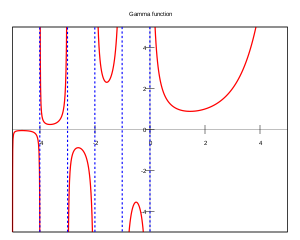
Reálná část Γ(z)
Imaginární část Γ(z)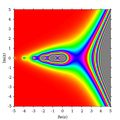
Absolutní hodnota Γ(z)
Absolutní hodnota Γ(z), 3D pohled
