Biangulární souřadnice jsou soustava souřadnic v rovině určená úsečkou , kde poloha bodu je určena dvěma úhly . Tento typ souřadnic jako první zkoumal Lazare Nicholas Marguerite Carnot , který své výsledky publikoval v roce 1803.[ 1]
Poloha bodu
V rovině je dána úsečka A B ¯ {\displaystyle {\overline {AB}}\,\!} C {\displaystyle C} přímce A B ¯ {\displaystyle {\overline {AB}}\,\!} ∠ C A B {\displaystyle \angle CAB\,\!} ∠ C B A {\displaystyle \angle CBA\,\!}
Polohu bodů na přímce A B ¯ {\displaystyle {\overline {AB}}\,\!} ∠ C A B {\displaystyle \angle CAB\,\!} ∠ C B A {\displaystyle \angle CBA\,\!} přímé (180°).
Máme bod, zvaný C {\displaystyle C}
Definice bodu c úhlovými souřadnicemi α a β v rovině. Zvolme v rovině úsečku A B {\displaystyle AB} C {\displaystyle C}
Najdeme úhly α {\displaystyle \alpha } β {\displaystyle \beta } C A B {\displaystyle CAB} C B A {\displaystyle CBA}
Úsečka A B {\displaystyle AB} α {\displaystyle \alpha } β {\displaystyle \beta } α {\displaystyle \alpha } β {\displaystyle \beta }
x = c t g β t g α + tg β {\displaystyle x={\frac {c\ \operatorname {tg\,} \beta }{\operatorname {tg\,} \alpha +\operatorname {tg} \beta }}}
y = c t g α t g β t g α + t g β {\displaystyle y={\frac {c\,\operatorname {tg\,} \alpha \,\operatorname {tg\,} \beta }{\operatorname {tg\,} \alpha +\operatorname {tg\,} \beta }}}
a pro zpětný převod souřadnic x-y na α - β použijeme rovnice:
α = arctg2 ( y x ) , {\displaystyle \alpha =\operatorname {arctg2} \left({\frac {y}{x}}\right),}
β = arctg2 ( y c − x ) , {\displaystyle \beta =\operatorname {arctg2} \left({\frac {y}{c-x}}\right),}
kde arctg2 je zobecnění funkce arkus tangens často užívané při inverzích vztahů v rovině.
V úhlových souřadnicích se dá jednoduše vyjádřit rovnice jistých kuželoseček v rovině.
Rovnice elipsy :
t g β = 1 t g α + 1 , 5 {\displaystyle \operatorname {tg\ } \beta ={\frac {1}{\operatorname {tg\ } \alpha }}+1,5}
Rovnice paraboly :
t g β = 1 t g α + 2 {\displaystyle \operatorname {tg\ } \beta ={\frac {1}{\operatorname {tg\ } \alpha }}+2}
Rovnice hyperboly :
t g β = 1 t g α + 3 {\displaystyle \operatorname {tg\ } \beta ={\frac {1}{\operatorname {tg\ } \alpha }}+3}
Elipsa, definovaná úhlovými souřadnicemi v rovině
Parabola, definovaná úhlovými souřadnicemi v rovině
Hyperbola, definovaná úhlovými souřadnicemi v rovině
Reference
Zdroj
Poslední aktualizace obsahu: 2025-04-27 04:19:13
Zdroj: Wikipedia (autoři článku Úhlová soustava souřadnic )
Licence textu: CC-BY-SA-3.0 Unported
Tento článek byl automaticky přejat z Wikipedie. Na obrázcích nebyly provedeny žádné změny. Obrázky se zobrazují ve zmenšené velikosti (jako miniatury). Kliknutím na obrázek získáte další informace o autorovi a licenci. Byly změněny prvky designu, odstraněny některé odkazy specifické pro Wikipedii (např. odkazy na Editaci a nebo na neexistující hesla) a provedena optimalizace pro rychlé načítání.

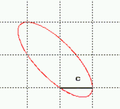 Elipsa, definovaná úhlovými souřadnicemi v rovině
Elipsa, definovaná úhlovými souřadnicemi v rovině Parabola, definovaná úhlovými souřadnicemi v rovině
Parabola, definovaná úhlovými souřadnicemi v rovině Hyperbola, definovaná úhlovými souřadnicemi v rovině
Hyperbola, definovaná úhlovými souřadnicemi v rovině



















