Přechodový jev (elektrický obvod)
Přechodový jev je fyzikální děj probíhající v čase mezi dvěma ustálenými stavy. V ustáleném stavu se energie soustavy nemění (popř. se mění periodicky), během přechodového děje dochází k jejím změnám.
Vznik jevu je podmíněn změnami energie v akumulačních prvcích obvodu (kondenzátory a cívky). Tyto změny nemohou proběhnout okamžitě, protože by vyžadovaly zdroj nekonečné energie. Charakter jevu závisí na druhu zapojených akumulačních prvků. Obsahuje-li obvod pouze jeden akumulační prvek obvodu (tj. kromě rezistoru pouze kondenzátor nebo pouze cívku), nemůže dojít k vratné výměně energie a děj probíhá aperiodicky. Pokud však obvod obsahuje oba akumulační prvky, dochází k periodické výměně energie mezi prvky - rezonance. Tyto obvody pak nazýváme oscilátory.

Přechodové jevy prvního řádu
RL obvod

RL obvod je tvořen zdrojem stejnosměrného elektrického napětí a sériovým zapojením ideálního rezistoru a ideální cívky. Po připojení ke zdroji začne obvodem procházet elektrický proud, který na cívce vytvoří magnetické pole, které se bude zvětšovat a na cívce se začne indukovat napětí. Napětí na cívce je zpočátku stejně velké jako napětí zdroje, zatímco napětí na rezistoru je rovno nule. Postupně se však bude napětí na cívce snižovat a na rezistoru zvyšovat až bude obvodem protékat ustálený proud jako řešení rovnice (2.Kirchhoffův zákon):
- tj. tj. tj.
a po odpojení zdroje napětí se začne energie magnetického pole cívky měnit v rezistoru na energii tepelnou:
- tj. tj. tj. ,
časová konstanta je .
RL obvod (střídavý)

RL obvod je tvořen zdrojem střídavého elektrického napětí a sériovým zapojením ideálního rezistoru a ideální cívky a je modelován rovnicí (2.Kirchhoffův zákon):
- tj. tj. tj.
kde a představuje úhlovou frekvenci střídavé třífázové sítě ( viz výše). Uvedené řešení diferenciální rovnice je východiskem výpočtů zkratových poměrů v třífázových elektrizačních soustavách, viz norma ČSN EN 60909-0 ED.2 (333022).
RC obvod


RC obvod je tvořen zdrojem stejnosměrného elektrického napětí a sériovým zapojením ideálního rezistoru a ideálního kondenzátoru. Po připojení ke zdroji začne obvodem procházet elektrický proud, který na kondenzátoru vytvoří elektrické pole, které se bude zvětšovat a kondenzátor se začne nabíjet (bude v něm vzrůstat nahromaděný náboj). Napětí na rezistoru je zpočátku stejně velké jako napětí zdroje, zatímco napětí na kondenzátoru je rovno nule. Postupně se však bude napětí na rezistoru snižovat a na kondenzátoru zvyšovat až bude obvodem protékat ustálený proud jako řešení rovnice (2.Kirchhoffův zákon):
- .
Tuto rovnici je nutné derivovat podle času t, dostáváme rovnici prvního řádu:
- tj. tj. tj.
a po odpojení zdroje napětí se začne energie elektrického pole kondenzátoru měnit v rezistoru na energii tepelnou:
- tj. tj. tj. ,
kde časová konstanta je , tj. za čas se kondenzátor nabije zhruba na dvě třetiny své kapacity a za čas se kondenzátor nabije na 95% své kapacity, kondenzátor pak lze považovat za nabitý. Vybíjení kondenzátoru probíhá reverzně k nabíjení.
Lineární pasivní elektrický RC obvod měnící signál v závislosti na kmitočtu se užívá jako frekvenční filtr, např. horní propust nebo dolní propust.
Přechodové jevy druhého řádu
LC obvod
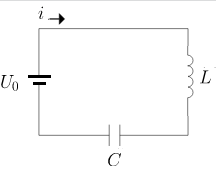
LC obvod je tvořen zdrojem stejnosměrného elektrického napětí a sériovým zapojením ideální cívky a ideálního kondenzátoru a je modelován rovnicí (2.Kirchhoffův zákon):
- .
Tuto rovnici je nutné derivovat podle času t, dostáváme rovnici druhého řádu:
- tj. - pro
kde představuje rezonanční úhlovou frekvenci netlumeného kmitání.
RLC obvod

RLC obvod je tvořen zdrojem stejnosměrného elektrického napětí a sériovým zapojením ideálního rezistoru (odporu), ideální cívky (indukčnosti) a ideálního kondenzátoru (kapacity) a je modelován rovnicí (2.Kirchhoffův zákon):
- .
Tuto rovnici je nutné derivovat podle času t, dostáváme rovnici druhého řádu:
- tj. - pro a
a kde pro představuje úhlovou frekvenci tlumeného kmitání.
Charakteristická rovnice výše uvedené homogenní diferenciální rovnice je ve tvaru:
- tj.
a pro diskriminant uvedené kvadratické rovnice platí:
- řešením jsou dva různé reálné kořeny a a děj je aperiodický
- řešením jsou dva shodné reálné kořeny a děj je na mezi periodicity
- řešením jsou dva kořeny komplexně sdružené a děj je periodický (viz řešení výše uvedené diferenciální rovnice).
RLC obvod (střídavý)

RLC obvod je tvořen zdrojem střídavého elektrického napětí a sériovým zapojením ideálního rezistoru, ideální cívky a ideálního kondenzátoru a je modelován rovnicí (2.Kirchhoffův zákon):
- .
Tuto rovnici je nutné derivovat podle času t, dostáváme rovnici druhého řádu:
a kde představuje úhlovou frekvenci kmitání střídavého napětí.
Řešení výše uvedené rovnice ve tvaru:
- tj. tj.
dosaďme do výše uvedené rovnice, pak dostaneme:
- tj. tj. .
Související články
Externí odkazy
- Obrázky, zvuky či videa k tématu přechodové jevy na Wikimedia Commons
- Sériový RLC obvod (anglicky)
- Sériový RLC obvod (anglicky) Archivováno 23. 9. 2022 na Wayback Machine.
- Miloš Křivan: Matematický model elektrické sı́tě




















































